|
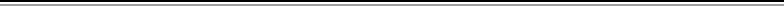
フォト_ギャラリー
2021年02月10日 [ 第620回 ]
エナガ,アトリ,イカル,余録;レンズのコマ収差
|
|


エナガ Long-tailed Tit Aegithalos caudatus
分類:スズメ目 エナガ科
全長:14.0cm
翼開長:16.0cm
分布:九州以北で留鳥または漂鳥。
生息環境:平地〜山地の林など。
食性:昆虫、蜘蛛、木の実など。
フォトギャラリー:第611回他参照
撮影難易度:★★☆☆☆
撮影日:2021年2月1日
撮影時間:09時02分47秒
シャッタースピード:1/250秒
絞り値:F5.6
撮影モード:絞り優先AE
焦点距離:300mm(換算450mm)
ISO感度:800
撮影地:大阪府
使用カメラ:NIKON D5100
使用レンズ:Nikon AF−S NIKKOR55−300mm 1:4.5−5.6G ED VR
撮影日:2021年2月1日
撮影時間:09時03分09秒
シャッタースピード:1/125秒
絞り値:F5.6
撮影モード:絞り優先AE
焦点距離:300mm(換算450mm)
ISO感度:800
撮影地:大阪府
使用カメラ:NIKON D5100
使用レンズ:Nikon AF−S NIKKOR55−300mm 1:4.5−5.6G ED VR

アトリ(雌タイプ) Brambling Fringilla montifringilla
分類:スズメ目 アトリ科
全長:16.0cm
翼開長:25.5cm
分布:全国で冬鳥。
生息環境:平地〜山地の草原、林など。
食性:木の実、種子など。
フォトギャラリー:第607回他参照
撮影難易度:★★☆☆☆
撮影日:2021年2月1日
撮影時間:10時52分33秒
シャッタースピード:1/1250秒
絞り値:F5.6
撮影モード:マニュアル
焦点距離:300mm(換算450mm)
ISO感度:800
撮影地:大阪府
使用カメラ:NIKON D5100
使用レンズ:Nikon AF−S NIKKOR55−300mm 1:4.5−5.6G ED VR

イカル Japanese Grosbeak Eophona personata
分類:スズメ目 アトリ科
全長:23.0cm
翼開長:33.0cm
分布:九州以北で留鳥または漂鳥。
生息環境:平地〜山地の林など。
食性:草木の種子など。
フォトギャラリー:第573回他参照
撮影難易度:★★☆☆☆
撮影日:2021年2月1日
撮影時間:10時53分58秒
シャッタースピード:1/3200秒
絞り値:F5.6
撮影モード:絞り優先AE
焦点距離:300mm(換算450mm)
ISO感度:800
撮影地:大阪府
使用カメラ:NIKON D5100
使用レンズ:Nikon AF−S NIKKOR55−300mm 1:4.5−5.6G ED VR

カケス(亜種カケス) Eurasian Jay Garrulus glandarius japonicus
分類:スズメ目 カラス科
全長:33.0cm
翼開長:50.0cm
分布:本州、四国、九州などで留鳥または漂鳥。
生息環境:平地〜山地の林。
食性:木の実など。
フォトギャラリー:第609回他参照
撮影難易度:★★☆☆☆
撮影日:2021年2月1日
撮影時間:08時22分53秒
シャッタースピード:1/500秒
絞り値:F5.6
撮影モード:マニュアル
焦点距離:300mm(換算450mm)
ISO感度:800
撮影地:大阪府
使用カメラ:NIKON D5100
使用レンズ:Nikon AF−S NIKKOR55−300mm 1:4.5−5.6G ED VR
最近入り浸っている自宅近くのフィールドの先でエナガの群れが至近距離で撮れた。 目の前と言っ
ても良い距離感で戯れてくれたので存分に撮影出来た。 調子に乗ってちょっと先まで足を延ばしたが
その甲斐無くまた戻って来たらアトリの仲間2種がほぼ同時に撮れた。 混群だった訳ではないがほぼ
同じ場所にアトリとイカルが居た。
この日初めに撮れていたのは実はカケスだった。 正確な撮影ポイントは記憶が曖昧だが自宅を出
て間もなくには違いない。 最近贅沢さえ言わなければ自宅付近で探鳥が完結してしまうので遠くまで
足を延ばすのが馬鹿らしく思える程だ。
余録;レンズのコマ収差
前回まで色収差、球面収差について取り上げて来た。 今回は球面収差と似ているがコマ収差につ
いてお勉強。 前回までの図は無限遠からの光線を表していたが上図は無限遠の手前からの光束を
表している。 ここで言う「光線」とは面積を持たない点光源(ほぼ無限遠の恒星の光など)からの点像
を表す一方「光束」とは面積を持った光の束として表現される。 左端の矢印形の物体OPが右端の撮
像素子やフィルム(以下まとめて「撮像素子」と言う)にどう結像するかというのが図の意味だ。 因みに
ベテランの人はご存じと思うがカメラの撮像素子には上下左右が反転して投影される。 入射瞳の端を
通る光束が中心付近を通った光束の結像O'P'とは倍率の異なる像O'P''を結像するのがコマ収差だ。
本来なら点で結像しなければならない物体(P)も倍率の差P'−P''分だけ面となって広がり非対称な
ボケとなって現れる。
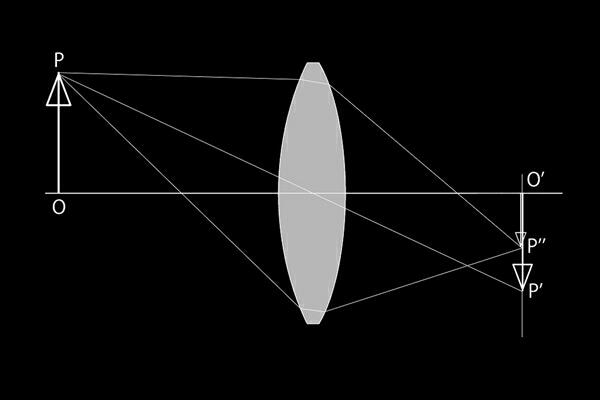
▲ 無限遠付近からの平行な光線のコマ収差
ほぼ無限遠の恒星などからの平行な光線も光軸に対し斜めに入射するとコマ収差によって面積を持
ち主光線の片側へ彗星の尾の様な形にボケる。 その形が独楽みたいだからコマ収差と言うのだろう
か。 この収差を補正するには瞳の全域で倍率を主光線のP'に一致させねばならない。 そのための
条件として導き出されたのが正弦条件というものだ。
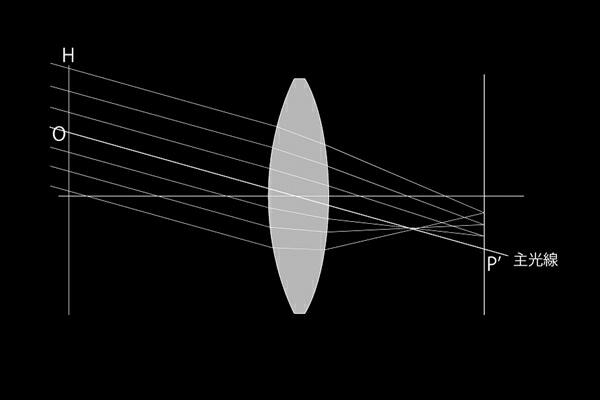
▲ 正弦条件
瞳の全域で倍率を主光線のP'に一致させるという事はあらゆる入射高の倍率が主光線の倍率と同じ
という事だから
sinu÷sinu'=β
(u:物体側の軸上光線の傾角 u':像側の軸上光線の傾角 β:近軸倍率)
という関係が成立するという事だ。
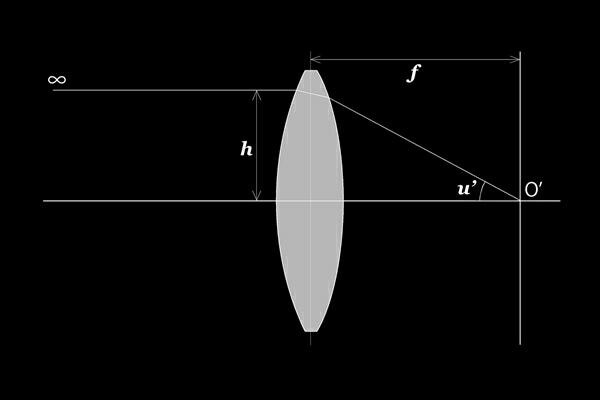
物体が無限遠の時はsinuとhが、近軸倍率βと焦点距離fがそれぞれ等しくなるので
h÷sinu'=f
(h:入射光の高さ f:焦点距離)
という式に変換される。
従って各入射光の高さhごとの主光線との倍率のズレ(不満量)S.C. は
S.C.=(h÷sinu')−f
(h:入射光の高さ u':像側の軸上光線の傾角 f:焦点距離)
で表される。
という難しい公式のS.C.をゼロに近づけると軸上からあまり離れていないコマ収差がある程度除去さ
れるという理屈になる(画面の全域にわたって完全にゼロにする事は出来ない)。
今回はかなり難しい話になってしまったが次回は更に難解な非点収差について。
参考文献:小倉敏布「写真レンズの基礎と発展」朝日ソノラマ社1998年
|
|
|
|